 |
| regristration of a scan dying |
– hi Coats
– hi Rez
– what’s up, Coats?
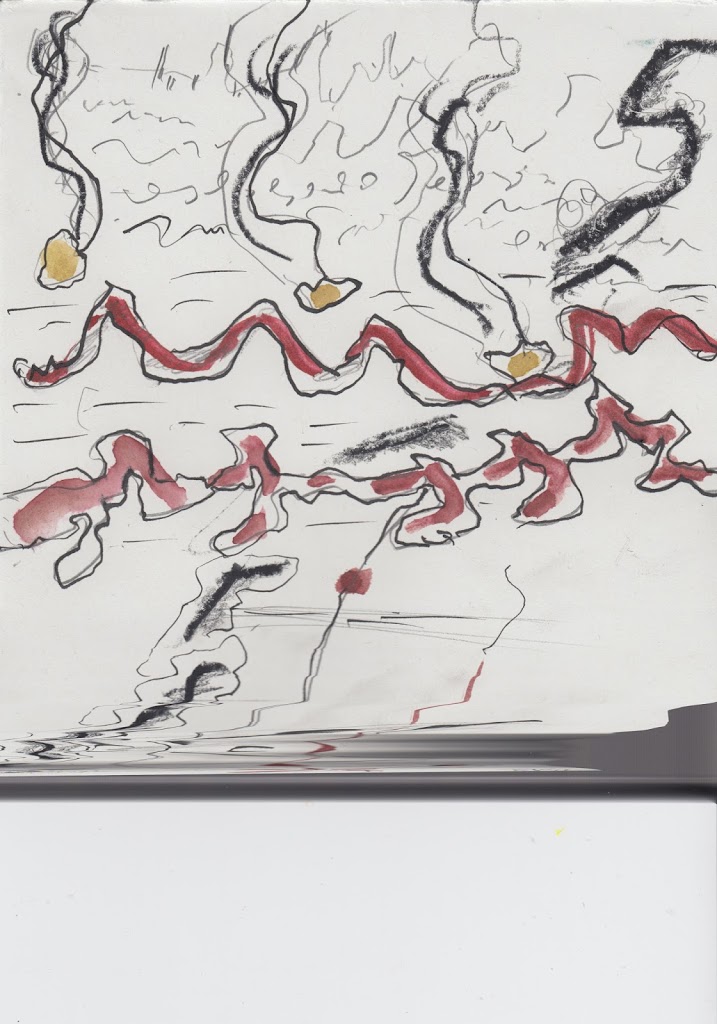
– nothing much, Rez. Yesterday, i was scanning a drawing i made, but while the scan was running i realized i had forgotten something and removed the drawing from under the functioning scanner. and, well come over here and see, you can see all of that really happening on the completed scan. You see the black line: the scanner naturally keeps scanning but just above where it gets all black from opening the lid, so the light fades into the room, there you can actually see the drawing leaving the scan as it were, till there’s no drawing left. You see what you get there is actually an horizon of the scan’s existence, pretty cool huh?
– hm, yeah, so I guess you didn’t call me in about the image or about the scanner that’s broke or something? I ain’t buying you a new scanner if that’s what you ‘re after
– heck no Rez, the scanner’s fine, i just wanted to talk to you about the scan itself cause i think it’s rather cool, as if it was a life, starting with me clicking the ‘Scan’ button in my scan software that triggered the scan procedure. So you see i ‘m thinking of the act of clicking as the time of conception of the scan, and the scan’s birth would be when the drawing is reached by the scans lamplight, and its premature death would have occurred when i pulled the drawing away from the light.
– why do you want to think of it that way? isn’t that a bit morbid? or, er, silly? I mean, christ it’s just a scan…
– i don’t know, it’s an experiment, ..i thought it was somehow important when it happened and when i saw the resulting image .. i thought well hey this image is really telling me something…
– so now you’re saying the scan was talking to you? have you been drinking Coats…
– hahaha no, Rez, no of course not, the scan wasn’t really something with a consciousness or anything but now that you mention it, speaking metaphorically, what if it was?
– talking to you?
– no silly: what if we think of the scan as a lifetime of a conscious being and of the act of me ripping away the image as of its violent and premature death. Let’s do a thought experiment here. A ‘normal’ scan with a ‘natural death’ would have resulted in a clean image, a digital representation of the image.
– yes, now i see what you’re getting at: so it’s not the image that died here, and neither is it the scan as in ’the file containing the scanned data’ but the process of scanning itself?
– exactly.You see we think of things all the time, preferably things we can touch and hold in our hands but if that’s not the case we think of things anyway and just pretend they are things , like the ‘scan’ is a thing while it’s actually just a bunch of data in a computer file, and we entirely disregard the process of scanning in favor of whatever it is we can get to grips with: the image on the screen, the drawing, the scanner, the computer. But we entirely disregard what is happening, the process at hand, what is going on…
– well that’s obvious, isn’t it: things you can see but what happens is more elusive, you can only talk about what happens, well by talking about the things that are happening or to which whatever happens is happening…
– yes i agree it is obvious. It’s a pity though…
– what for? what’s the trouble with things?
– nothing, i guess. It’s just that…well…what is it that dies when we die?
– oh dear! Now that’s a surprise, i didn’t see that one coming! what on earth do you mean?
– well it’s not the body that dies, is it? The body just stops functioning as a body, it is no longer the required support for ‘having’ life, all of it’s subroutines quit and that’s that.If nobody does anything it will just rot away, but it could keep functioning with some aid, at least parts of it could. So we don’t say ’that body has just died’…
– hm pretty bleak, but yes , i suppose so. It’s more the brain that dies isn’t it. That’s what they say that counts as time of death, isn’t it, when the dead or dying person is ‘brain dead’…?
– no please, no no, for the moment i do not want to go into all those technicalities of death, and neither do i want to tackle those controversial discussions on near death experiences and the ‘consciousness surviving brain death’ thing. Let’s go into that only and i mean only when we actually really need to, there’s too many issues involved there and lots of sensationalist humbug.
One step at a time, please, we ain’t nearly dead yet, i hope.
– owkay Coats i’ll humor you, not that i see any valid reason to do so, but it’s a bright morning and it’s kinda cosy in here with sun falling into these layers of dusty books, dust and dirt and dirty books and lettuce, my god Coats do you ever clean up this place?
– in due course, rez, i clean the house in due course and might i remind you that sure you live here too.
for the time being let’s stick to the main issue here, and see how far we get., my first point being that it’s a very difficult question to answer in any sensible way is what it is that actually dies when a person dies. Because if you reduce the problem and say well it’s the brain that dies, so you disregard all of the rest of the person’s body